Created with Microsoft PhotoDraw 2000 v2

A handy rule (Rule 1):

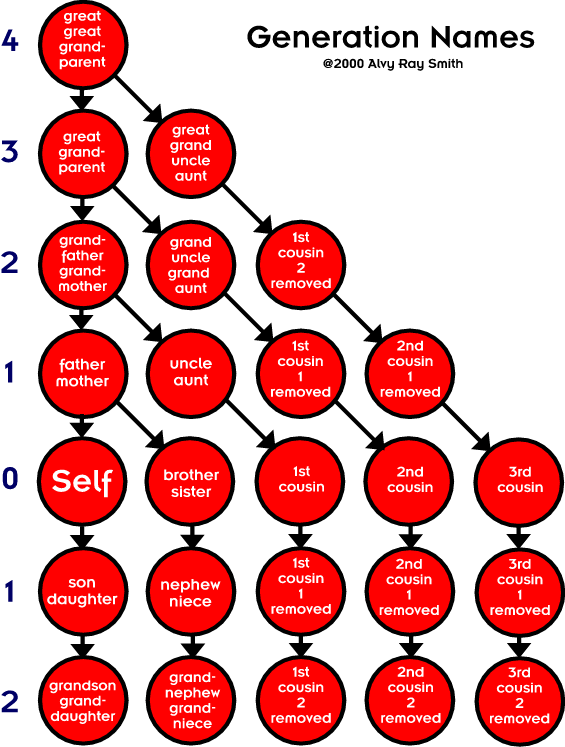
nth cousins share a gg...g [n times] parent.

For example, 1st cousins share a gparent [grandparent]; 2nd cousins share a ggparent [great-grandparent]; 3rd cousins share a gggparent [great-great-grandparent]; etc. Another way to say the same thing uses an exponent to indicate the repetition count of the "g"s (Rule 1 again):

nth cousins share a gⁿparent.

Another handy rule (Rule 2):

You are n+1 generations removed from your gⁿparent.

That is: Your generation count is 1 more than your "g" count. This is easy to see: You are 2 generations removed from any grandparent (gparent, with 1 "g").

A handy algorithm (that uses only Rule 1):

If you know that you, say Joe, have a gⁿparent in common with someone's, say Mary's, g^mparent, then you can compute the relationship of Joe to Mary this way: (I should also say that this assumes there is no nearer common ancestor)

1. Assume n > m. You can always reverse the roles if this is not true. If n = m, then just use Rule 1 above: Joe and Mary are mth cousins (or equivalently, nth cousins).

2. Find someone in Joe's line in the same generation as Mary. Let's say it is Sally (it doesn't matter who it is). Use the formula above to compute cousinhood: Sally and Mary are mth cousins. The short form of this step is, simply:

The first half of your answer is "mth cousin ..." (where m, recall, is the smaller of m and n).

3. Now determine how many generations separate Joe and Sally. Suppose it is p generations. Then Joe is Sally's mth cousin, p removed. The short form of this step is, simply:

The second half of your answer is "... p removed" (where p is n - m).

An exercise (that uses both Rule 1 and Rule 2):

I met a relative recently who was 5 generations down from our nearest common ancestor, and I was 8 generations down from the same ancestor. The relative's name was Lydia [not her real name]. "What is our relationship?" she asked.

Here's how I computed it. First I determined m and n. They are not 5 and 8 as you might first assume. The generation count is not the same as the number of "g"s in front of "parent".  Here's where you use Rule 2. So my g⁷parent is in common with Lydia's g⁴parent. So some direct ancestor of mine in the 5th generation with Lydia is her 4th cousin. It doesn't matter who that person is. Determining p (the "remove") is a snap. It's just 8 - 5 (or 7 - 4) equals 3. p is just the difference in generations between Lydia and me. So she and I are 4th cousins, 3 removed (or "3 times removed", or "thrice removed").